Nです.今回は相関と共分散がほとんど同じものを計算しているということをお伝えしたいと思います.相関と共分散の違いは期待値を計算する前に平均を引くかどうかですがそれを数式を使ってもう少し丁寧に説明したいと思います.
相関 (Correlation)
確率変数\(X_1, X_2\)があるとき,その相関は
$$ \mathrm{E} \langle X_1 X_2^\mathrm{T} \rangle, $$
で表されます.
\(X_1, X_2\)がスカラーな確率変数だとすると期待値計算は次のように実現値とその実現値が起きる確率の掛け算を積分した値になります.
$$ \mathrm{E} \langle X_1 X_2^\mathrm{T} \rangle = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} X_1X_2 p[X_1,X_2]dX_1dX_2.$$
数式だけではイメージがつかないという方は次の図を見てください.
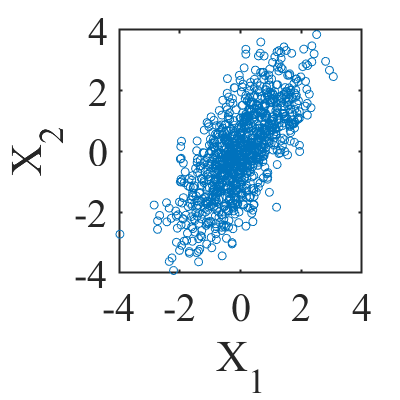
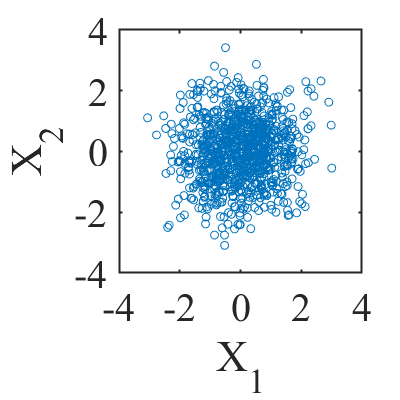
こんな感じの図を見たことがある人は多いと思います.
散布図に何かしらの偏り(例えば直線的に分布が伸びているとか)があるときその偏りに直線を当てはめます.
そのときに正の傾きがあれば正の相関がありそうだし,負の傾きなら負の相関があるし,分布が左右上下に対称なら相関がなさそうだなと直感的に思うわけです.
図1のように分布が偏っていれば例えば\(X_1=2\)のときに\(X_2\)は2ぐらいだろうなと予測できます.つまり正の相関とは確率変数\(X_1\)が大きなときには\(X_2\)も大きく, \(X_1\)が小さなときには\(X_2\)も小さくなるということを意味しているわけです.
この偏りは上記の式の\(p[X_1, X_2]\)に反映されます. \(p[X_1, X_2]\) はある \(X_1\) と \(X_2\)が出る確率です.正の相関を持つ場合 \(X_1\)が大きなときには\(X_2\)も大きくなりやすい,つまり大きな \(X_1\) と \(X_2\) が出る確率 \(p[X_1, X_2]\) が大きくなりそれらの積分である相関も大きくなります.
このような形で上記の式は2つの確率変数の相関を計算することができるわけです.
確率変数が独立な場合の相関
確率変数 \(X_1\) と \(X_2\) が独立の場合その結合確率密度関数は
$$ p[X_1, X_2] = p[X_1] \times p[X_2],$$で表されます.
これを使って相関の定義式を次のように変形することができます
$$
\begin{align}
\mathrm{E} \langle X_1 X_2^\mathrm{T} \rangle &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} X_1X_2 p[X_1,X_2]dX_1dX_2 \\
&= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} X_1X_2 p[X_1]p[X_2]dX_1dX_2 \\
&= \int_{-\infty}^{\infty} X_1p[X_1]dX_1 \times \int_{-\infty}^{\infty} X_2p[X_2]dX_2 \\
&= \mathrm{E} \langle X_1 \rangle \times \mathrm{E} \langle X_2 \rangle .
\end{align}
$$
つまり確率変数 \(X_1\) と \(X_2\) が独立な場合その相関は確率変数 \(X_1\) の期待値(平均)と確率変数 \(X_2\) の期待値(平均)の掛け算となるわけです.
ここで注意していただきたいのは確率変数 \(X_1\) と \(X_2\) が独立な場合でもその平均値が0でない場合は相関は0にならないという点です.
そして 確率変数 \(X_1\) と \(X_2\) が独立な場合 に必ず0となるように相関を修正したものが共分散となります.
共分散 (Covariance)
共分散の定義は以下のようになっています.
$$ \mathrm{E} \langle [X_1 – \mathrm{E}\langle X_1 \rangle] [X_2 – \mathrm{E}\langle X_2 \rangle] ^\mathrm{T} \rangle. $$
相関と何が違うかというと各確率変数から平均値を引いてから期待値を計算しています.つまり\( X_1 – \mathrm{E}\langle X_1 \rangle \)の期待値は常に0になるので(あらかじめ引いているので当たり前ですが),独立な確率変数同士の共分散は常に0になるわけです.
まとめ
いろいろ書きましたが一言でいうと共分散は相関を確率変数が独立なときに必ず0になるように調整したものであるということです.
おまけ:MATLAB code
今回分布の図を作成するのに使用したMATLABのソースコードです.
x=randn(1000,1);
y=randn(1000,1);
figure('Position',[100 100 400 400])
scatter(x,y)
xlim([-4 4])
ylim([-4 4])
xlabel('X_1')
ylabel('X_2')
R = corrcoef(x,y)
figure('Position',[100 100 400 400])
scatter(x,y+x)
xlim([-4 4])
ylim([-4 4])
xlabel('X_1')
ylabel('X_2')
R = corrcoef(x,y+x)

コメント