Nです.今回はブラウザ上で有限要素法の計算を行うことができるFREEFEM++-JSというサイトについて紹介します.このサイトはパリのSorbonne大学のAntoine Le Hyaricが作成したサイトで,FREEFEM++というソフトと同じような有限要素法の計算をブラウザ上でできます.
詳しい解説はQiitaの”FreeFem++の紹介“という記事に乗っているので今回は遊んでみた結果を載せたいと思います.
まずFREEFEM++-JSのサイトに飛ぶと以下のような画面になります.最初からサンプルコードが書かれています.

とりあえず”Run”ボタンを押すと次のような計算結果が表示されます.これはPoisson’s方程式$$\frac{d^2u}{dx^2}+ \frac{d^2u}{dy^2}=f $$をディリクレ境界条件として境界の値0を使用した結果になっています.
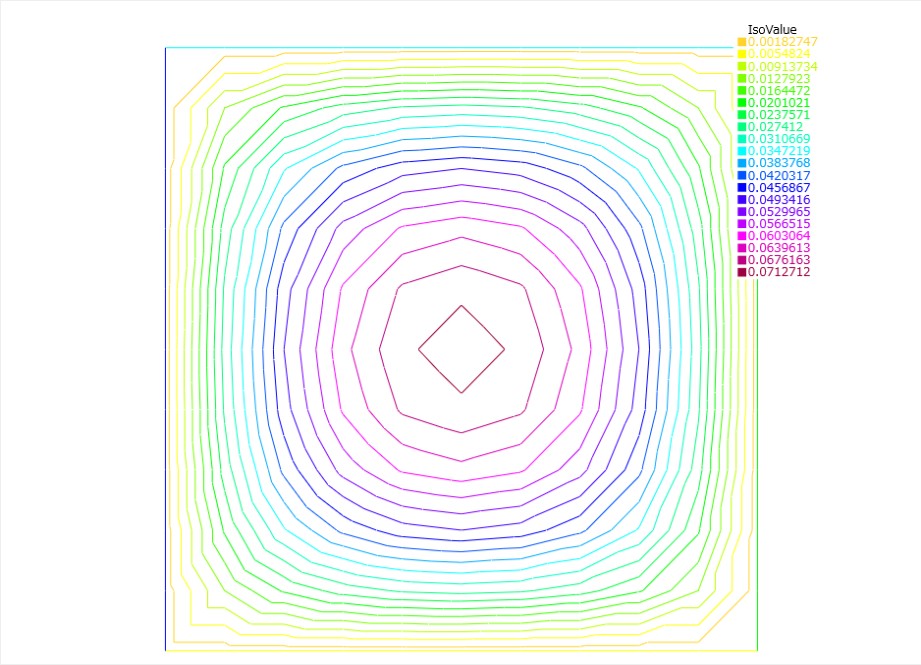
このサンプルコードについて説明したいと思います.
有限要素法を行うためには以下の5つのステップが必要となります.(1)領域をメッシュに分割,(2)有限要素空間の作成,(3)弱形式で微分方程式を記述し連立方程式を作成,(4)連立方程式を解く,(5)計算結果の表示.
(1)領域をメッシュに分割
サンプルコードでは(1)のメッシュに分割を
mesh Th=square(10,10);で行っています.
ためしにメッシュを
plot(Th,uh,value=true); // see the resultとコードの最後を書き替えて表示してみるときれいに分割されています(計算精度は実はメッシュの分割が単純でないほうが精度が高いらしいです).

(2)有限要素空間の作成
つぎにどのような基底関数を使って計算を近似するかを指定します.
fespace Vh(Th,P1); // P1 FE space今回は上記のように分割した要素に対してP1(区分的1次多項式,各格子点間の値は直線で近似しますよという意味です)を使用しています.このとき基底関数は三角要素の各頂点の高さが1になるような三角錐を考えているイメージです.
(3)弱形式で微分方程式を記述
次に解くべき微分方程式について記述します.
基本的には以下のように書きます.
問題の名前(近似空間の元,近似空間の元) = 弱形式 + on(境界の番号,Dirichlet境界条件);サンプルコードでも同じような感じになっています.ここでind2dは2次元の2重積分という意味です. 弱形式は$$\int\int v(\frac{d^2u}{dx^2}+ \frac{d^2u}{dy^2}-f )dxdy = 0 $$ を部分積分,もしくはグリーンの公式で次元を下げたものを書くみたいです.
Vh uh,vh; // Unkown and test function
func f=1; // Right hand side function
func g=0; // Boundary condition function
// Definition of the problem
problem laplace(uh,vh,solver=GMRES,tgv=1e5) =
int2d(Th)( dx(uh)*dx(vh) + dy(uh)*dy(vh) ) // bilinear form
- int2d(Th)( f*vh ) // linear form
+ on(1,2,3,4,uh=g) ; // boundary condition form実はこの段階で近似した微分方程式の境界値問題を解くことと連立方程式を解くことが等価になります.つまり$$ K\mathbf{u} = \mathbf{b}$$を解けばよくなっています.
(4)連立方程式を解く
$$ \mathbf{u} = K^{-1} \mathbf{b}$$ の計算をします.
これは(3)で定義したproblem 変数をそのまま書くだけでOKです.
laplace; // Solve the problem(5)結果の表示
plot()関数で結果を表示できます.
plot(uh,value=true); // see the result

コメント