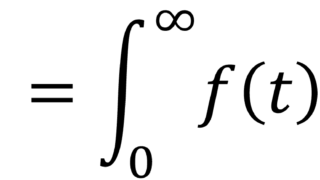 サイエンス
サイエンス 【システム制御工学1】ラプラス変換を理解する
ラプラス変換の気持ち なぜラプラス変換を学ぶのか?端的に言うとラプラス変換は微分方程式を誰でも解けるようにするツールである.微分方程式は物体の運動,電気回路,化学反応など自然界の現象を記述する際に必要不可欠で多くの場合その解を知ることが重要...
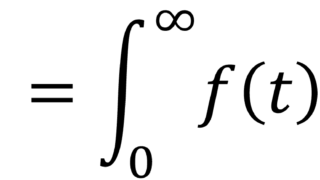 サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス  サイエンス
サイエンス