【コロナウイルス】偽陽性，偽陰性の点からどの程度の患者をRT-PCR法で検査すべきか【ベイズの定理】

2020年2月現在，コロナウイルスも検査法として Reverse Transcriptase – Polymerase Chain Reaction法 (RT-PCR法)が使用され，陽性，陰性が判断されているということがニュースでもよく話題に上がるようになっています．そして重要な問題として，RT-PCR検査を重症の患者に限って行うべきか，それとも軽症の患者にも行うべきかといった議論が存在します．

この論点を考える際の材料の一つにRT-PCR法の精度の問題があります．つまりコロナウイルスにかかっている人が100%陽性になるわけではないし（偽陰性），コロナウイルスにかかっていない人も陽性になってしまうこと（偽陽性）があるわけです．

今回は「RT-PCR法の精度と，検査をする人の中でコロナウイルスにかかっている人の割合からどのような問題が生じるのか」という点についてベイズの定理を使って考えていきたいと思います．

ベイズの定理について

まずベイズの定理について紹介します．ベイズの定理は以下の式で表されます

$$P(A|X) = \frac{P(X|A)P(A)}{P(X)},$$

このとき，\(P(\cdot)\)はかっこ内の事象が起こる確率を表しています．また括弧中の縦線“\(|\)”は条件付確率を表すときに用いられる記法で\( P(A|X) \)は\(X\)であるときに\(A\)となる確率を表しています．例えばP(真陽性|陽性)は検査で陽性になった人が本当に病気に感染している確率を表します．

ベイズの定理の導出について気になる方は「ベイズの定理の基本的な解説 | 高校数学の美しい物語」などを見てください．

コロナウイルスの例では\(X\)には検査の陽性，陰性，\(A\)にはその人が本当に陽性なのか陰性なのかつまり真陽性，真陰性という事象が対応します．

例としてPCR検査で陽性となった人が真陽性である確率を書くと以下のようになります

$$P(真陽性|陽性) = \frac{P(陽性|真陽性)P(真陽性)}{P(陽性)} .$$

もう少し日本語で書くと

$$陽性の人が真陽性である確率 = \frac{真陽性の人が陽性になる確率 \times 真陽性である人の割合}{検査した人の中で陽性となる人の割合} .$$

このとき検査した人の中で陽性となる人の割合は真陽性の人が陽性になる確率と，真陰性の人が陽性になる確率を足したものなので

$$P(真陽性|陽性) = \frac{P(陽性|真陽性)P(真陽性)}{ P(陽性|真陽性)P(真陽性) + P(陽性|真陰性)P(真陰性) } $$

とかけます．

以上の式から，陽性の人が真陽性である確率を求めるためには真陽性の人が陽性になる確率，つまりRT-PCR検査の精度と検査対象群における真陽性と真陰性の人の割合の２つが重要になります．

また以降では真陽性の人が陽性になる確率\( P(陽性|真陽性) \)を感度，真陰性の人が陰性になる確率\( P(陰性|真陰性) \)を特異度と呼びます．

現状のRT-PCR検査の推定精度（感度，特異度）

多くの人が直感的にわかるようにRT-PCR法の推定精度はどの程度の症状の人を検査対象にすべきか考える際に重要となります．

しかしながら，その人が真陽性なのか真陰性なのかは神様でもなければわかりません．そこで今回は中国の中南大学の研究グループの論文(Ai, Tao et al., 2020)の値を使って考えていきたいと思います．もし新型コロナウイルスのRT-PCRの精度（感度，特異度）について記述したよい論文ありましたら教えてください．

この論文内では1014人の患者に対してRT-PCRとCT検査の両方を行っています．その結果は以下の表のようになっています．

	CT検査　陽性	CT検査　陰性
RT-PCR法　陽性	580人	21人
RT-PCR法　陰性	308人	105人

今回，CT検査とRT-PCRの両方で陽性になった人を真陽性とし，両方陰性になった人を真陰性，片方陽性，片方陰性の人は0.5人真陽性，0.5人真陰性と仮定します．

注意点としてはこの論文ではRT-PCRの結果を正解として扱っているので今回の仮定は論文の趣旨とは外れています．また，この仮定には，コロナウイルスにかかった人がみな肺炎になるわけではない，また肺炎だからと言って必ずしもコロナウイルスによるものではないといった問題点が含まれていますが，新陽性か真陰性かは神様にしかわからないので今回のような仮定で大まかな数字を出してみたいと思います．

論文の結果から今回の仮定を利用すると

新陽性の人は\( 580+308/2+21/2=744.5人\)，また真陰性の人は \(308/2+21/2+105 =269.5人\) となります．

真陽性の人が陽性になる確率は
\( P(陽性|真陽性) = (580+10.5)/ 744.5 = 0.7931\)(感度)

真陽性の人が陰性になる確率は
\( P(陰性|真陽性) = 1 – 0.7931 = 0.2069\)

真陰性の人が陰性になる確率は
\( P(陰性|真陰性) = (154 + 105)/ 269.5 = 0.9610\) (特異度)

真陰性の人が陽性になる確率は
\( P(陽性|真陰性) = 1 – 0.9610 = 0.0390\)

検査を受けるグループにおける真陽性と真陰性 の人の割合

正直，真陽性と真陰性の人の割合は\( P(真陽性), P(真陰性)\)として表現されます．そしてこの確率はどの程度の人を対象に検査を行うかによって大きく変化します．以下では例として(1)日本人全員を調べた場合，(2)インフルエンザのような重い症状の人だけ検査した場合 ，(3)風程度の軽い症状の人も調べた場合について考えていきたいと思います．

正確な日本全体でコロナウイルスに感染している人数はわからないため，最悪を想定し，2月19日の中国の感染者数74185人とほぼ同じ人数，つまり日本に70000人，感染者（真陽性の人）がいると仮定します．以下ではこの仮定を使って検査対象の集団内の真陽性の人の割合を計算します．

(1)日本人全員を検査した場合

日本の人口はおよそ126800000人です．そのうち70000人がコロナウイルスにかかっているとすると
\( P(真陽性) = 70000/126800000 = 5.520 \times 10^{-4}\)，
また
\( P(真陰性) = 1 – P(真陽性) = 0.9994\)
となります．つまり，日本人全員を検査対象として検査した場合，検査対象のじつに99.9%が真陰性の人になります．

さらに，RT-PCRの特異度が96%であるということは，100人検査すると4人は真陰性であるにもかかわらず陽性になってしまうことを意味しています．もっというと，日本の人口126800000人が全て真陰性でコロナウイルスに感染していないときに検査をしても5072000人もの偽陽性の人が生じることになります．これは検査対象における真陽性の人の割合が小さいことの問題を如実に表しています．

ベイズの定理で検査で陽性の人が本当はコロナウイルスにかかっていない確率（偽陽性）を計算すると，\( P(真陰性|陽性) = 0.9889\)となります．

これはRT-PCR検査をして陽性だったとしても，本当にコロナウイルスにかかっている確率は1%程度しかないことを意味しています．これは特異度が100%でないことと検査対象に陰性の人が陽性の人の1万倍存在することに起因します．

また 偽陰性は\( P(真陽性|陰性) = 0.0001\)より， RT-PCR検査で陰性だった場合，99.99%の確率で本当にコロナウイルスに感染していないといえます．

(2)インフルエンザのような重い症状の人だけ検査した場合

ここでは病院で検査を受けるという考えのもとインフルエンザの患者とコロナウイルスにかかっている人が混じって検査を受けることを仮定します．薬局サーベイランスをいうwebページによると今年のインフルエンザの1週間の推定患者数は20万-60万程度なので，あいだをとって40万人とします．つまり47万人を検査対象とします．
このとき
\( P(真陽性) = 70000/470000 = 0.1489\)，
また
\( P(真陰性) = 1 – P(真陽性) = 0.8511\)
となります．
これは検査対象の15%程度が真陽性の人であることを意味しています．

このときベイズの定理で検査で陽性の人が本当はコロナウイルスにかかっていない確率（偽陽性）を計算すると，\( P(真陰性|陽性) = 0.2192\)となります．

つまりRT-PCR検査で陽性だった場合，80%程度の確率で本当にコロナウイルスに感染していることを意味しています．

また偽陰性は \( P(真陽性|陰性) = 0.0363\)より， RT-PCR検査で陰性だった場合，96.37%の確率で本当にコロナウイルスに感染していないといえます．

(3)風邪程度の軽い症状の人も検査した場合

Wikipediaによると風邪の原因となるウイルスの10%がインフルエンザらしいので10倍の400万人がRT-PCR検査を受けると仮定します． このとき
\( P(真陽性) = 70000/4070000 = 0.0172\)，
また
\( P(真陰性) = 1 – P(真陽性) = 0.9828\)
となります．

このとき偽陽性は\( P(真陰性|陽性) = 0.7373\)となります．

つまりRT-PCR検査で陽性だった場合，25%程度の確率で本当にコロナウイルスに感染していることを意味しています．

また偽陰性は \( P(真陽性|陰性) = 0.0038\)より， RT-PCR検査で陰性だった場合，99.62%の確率で本当にコロナウイルスに感染していないといえます．

まとめ

これまでの計算で「検査をする人の中でコロナウイルスにかかっている人の割合」が検査で陽性であることの重要性に大きな影響を与えることがわかりました．つまり，検査対象をうまく絞ることが重要になってきます．感染拡大初期ではその条件が，例えば武漢に行った人，もしくはその人に接触した人だったわけです．

特にRT-PCR法が感度79%，特異度96%のとき，インフルエンザ程度の症状の人を対象にした場合の計算から， 新陽性の人が検査対象の15%以上にすることで，検査で陽性の人の80%以上が真陽性であり，陽性であることの社会的重要性が大きくなることがわかりました．

これまで陽性であることの社会的重要性を上げるためには検査対象の真陽性である人の割合を大きくすることが大切であることを述べてきました．最後に，検査対象者の真陽性の人の割合を大きくするためには，無差別に検査をしない，検査を受けるかどうかは医者が症状を見て判断する（患者が判断しない）といったことが大切になってくるのではないかということを提案して終わりたいと思います．

おまけ

下図は感度79%，特異度96%を仮定した際の「検査対象内の真陽性の人の割合(true rate)」と「偽陽性(false positive)，偽陰性(true negative)」の関係を表しています．図より検査対照群内の真陽性率が上がるほど偽陽性である確率が減ることがわかります．偽陽性が20%以下になるためには検査対象の真陽性の人の割合を20％以上にする必要があることも図からわかります．一方偽陰性である確率は検査対照群内の真陽性率が上がるほど増えていきます．

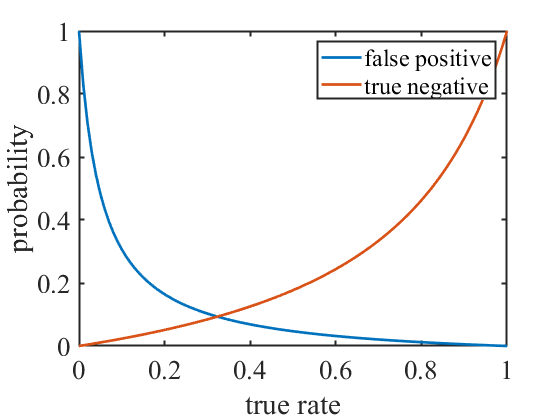
計算に使用したプログラム(MATLAB)

positive_true = (580+10.5)/ 744.5
negative_true = 1 - positive_true;
negative_false = (154 + 105)/ 269.5
positive_false = 1 - negative_false;
%% =====================================
% all_sample = 126800000 % all japan
% all_sample = 470000 % ful
all_sample = 4070000 % common cold
%% =====================================
infected_sample = 70000;

true_P = infected_sample/all_sample;
false_P = 1-true_P;

%true_positive = positive_true*true_P/(positive_true*true_P + positive_false*false_P)
false_positive = positive_false*false_P/(positive_true*true_P + positive_false*false_P)

true_negative = negative_true*true_P/(negative_true*true_P + negative_false*false_P)
%false_negative = negative_false*false_P/(negative_true*true_P + negative_false*false_P)

%% make figure =================================
dp = 100;

for i=1:dp+1
   true_P = (i-1)/dp;
   rate_true(i) = true_P;
   false_P = 1-true_P;
   false_positive(i) = positive_false*false_P/(positive_true*true_P + positive_false*false_P);
   true_negative(i) = negative_true*true_P/(negative_true*true_P + negative_false*false_P);
end

plot(rate_true,false_positive)
hold on
plot(rate_true,true_negative)
hold off
legend("false positive","true negative")
xlabel("true rate")
ylabel("probability")
% chenge font size==========
fontsize=20; 
h=gca; 
set(h,'fontsize',fontsize)
% ==========================

参考文献

ベイズの定理の基本的な解説 | 高校数学の美しい物語

Ai, Tao, Zhenlu Yang, Hongyan Hou, Chenao Zhan, Chong Chen, Wenzhi Lv, Qian Tao, Ziyong Sun, and Liming Xia. “Correlation of Chest CT and RT-PCR Testing in Coronavirus Disease 2019 (COVID-19) in China: A Report of 1014 Cases.” Radiology, February 26, 2020, 200642. https://doi.org/10.1148/radiol.2020200642.

薬局サーベイランス

風邪 – Wikipedia