Nです.今回はフーリエ変換についてまとめました.
離散フーリエ変換
離散フーリエ変換を行列で表すと以下の式のようになります.
\[ \left(
\begin{array}{c}
\hat{f_1} \\
\hat{f_2} \\
\hat{f_3} \\
\vdots \\
\hat{f_n}
\end{array}
\right)
=
\left(
\begin{array}{ccccc}
1 & 1 & 1 & \ldots & 1\\
1 & \omega_n & \omega_n^2 & \ldots & \omega_n^{n-1} \\
1 & \omega_n^2 & \omega_n^{2\times 2} & \ldots & \omega_n^{2(n-1)} \\
\vdots & \vdots& \vdots & \ddots & \vdots \\
1 & \omega_n^{n-1} & \omega_n^{(n-1)2} & \ldots & \omega_n^{(n-1)(n-1)}
\end{array}
\right)
\left(
\begin{array}{c}
f_1 \\
f_2 \\
f_3 \\
\vdots \\
f_n
\end{array}
\right) \\
\boldsymbol{\hat{f}} = F\boldsymbol{f}
\]
ここで,\(f_t\)はフーリエ変換の対象となる時系列,\(\hat{f_m}\)はフーリエ係数を表しています.また,\(\omega_n^i=e^{-2\pi i/n}\)でデータ長nに応じた基本周波数の第i高調波を表します.
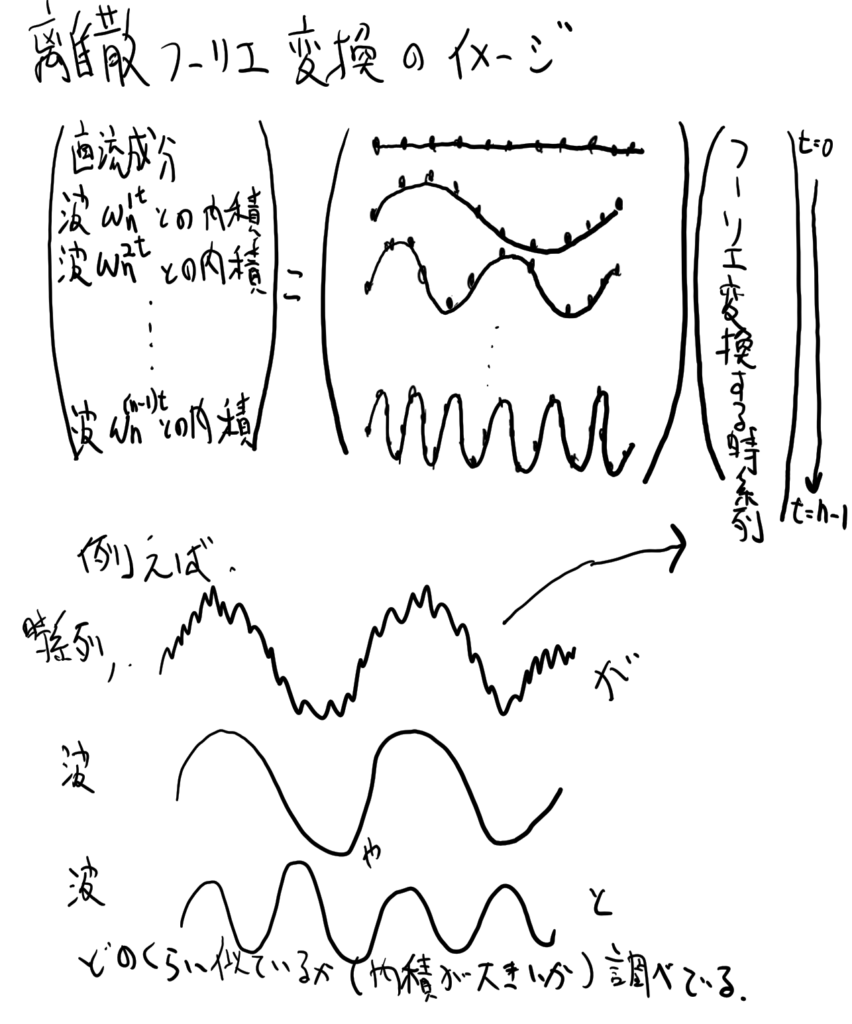
行列とベクトルの掛け算は行列の各行とベクトルの内積をたくさん計算するのと同じです.
そして内積は2つの時系列の類似度を表します.
つまり内積が類似度を計算しているという観点から離散ふーり

コメント