【MATLAB】Robotics Toolbox モデルパラメータの設定とシミュレーション編

Robotics Toolboxを理解するために簡単な倒立振子のシミュレーション（制御トルクなし）をRobotics Toolboxと自作プログラムの両方でおこない答えが一致することを確認していきます．

Robotics Toolboxのリンクのパラメータの設定方法についてあまりネットで調べても出てこなかったの自分用もかねてまとめました．

倒立単振子モデルのシミュレーション
1. コード1: モデルの作成
2. コード2: 作成したモデルのシミュレーション
自作2次元シミュレーションとの比較検証
1. コード3: Robotics toolboxを使わずに2次元の振子シミュレーションを作成
おまけ1: 常微分方程式を解いてくれるode45について
おまけ2: 自作SIP関数の説明

倒立単振子モデルのシミュレーション

コード1: モデルの作成

hight = 2.0; %[m] リンクの長さ
total_mass = 60; %[kg] リンクの重さ
I = [0 (total_mass*hight^2)/12 (total_mass*hight^2)/12];
r = [-1.0 0 0];

L1 = Link('d', 0,...　　%Denavit-Hartenberg(DH) パラメータ(リンク軸距離)
    'a', hight,...      %DH パラメータ (リンクの長さ)
    'alpha', 0,...      %DH パラメータ (リンクのねじれ角)
    'offset', pi/2,...  %角度のオフセット(theta = 0 の時に直立姿勢になるように調整)
    'm', total_mass,... %リンクの質量
    'I', I,...          %リンクの慣性モーメント
    'r', r);            %リンクのCoG位置

body = SerialLink([L1],...  %モデル作成に仕様するリンク
    'name', 'body',...      %モデルの名前
    'base',trotx(pi/2))     %１つ目のジョイントの姿勢

% 以下図のプロット用
theta = [0];
figure()
body.plot(theta) %角度θでプロット

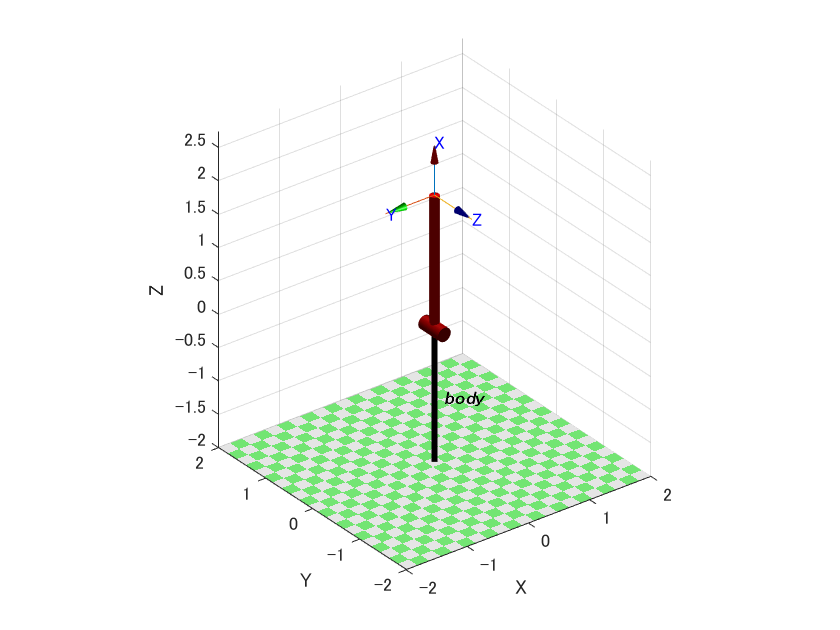
コード1を実行すると図1が作成できます．

Denavit–Hartenberg(DH) パラメータというのはあるリンクとジョイントがどのような状態でひとつ前のリンクにつながっているかを記述する際に使用されるパラメータです．今回はリンクの長さaを2 [m]に設定しました（今回はシンプルなモデルなのでd,alphaは0）．

rはリンクの質量中心(Center of Gravity；CoG)の位置です．図1のリンクの先端がリンクローカル座標系の原点となっています（これを理解するのに時間を浪費したのでここが結構伝えたいポイントです）．r = [x, y, z]=[-1, 0, 0]と設定すると，CoGはこの2[m]のリンクの中心となります．ここが間違えやすいポイントで例えばジョイント位置が原点だと考えてr=[+1, 0, 0]とすると後々の計算が合わなくなります．

慣性行列はリンクのCoG周りの慣性行列です．今回の計算に使用するのは主にZ軸まわりの慣性モーメントですが，リンクの中心周りの質線？(厚みのない棒)の慣性モーメントは\(\frac{mh^2}{12}\)です．今回のシミュレーションには影響しませんがY軸まわりの慣性モーメントもZ軸と同じです．一方X軸まわりの慣性モーメントは，質線には厚みがない（質量の分布がX軸上にしかない）ため0です．

図1: コード1を実行して作成した倒立振子モデル．**リンク座標系の原点はリンクの先端にあります．**

コード2: 作成したモデルのシミュレーション

%初期姿勢状態
q0 = [0.3];
qd0 = [0];
% 制御パラメータ（今回は制御なし）
P = 0;
D = 0;
% シミュレーション
[t,q,qd] = body.nofriction().fdyn(10, @(body, t, q, qd) tfunc(q, qd, qstar, P, D),q0,qd0 );

% ローカル関数
function tau = tfunc(q, qd, qstar, P, D)
   tau = 0.0; %制御トルクなし
end

このコード2をコード1の後に実行すると以下の動画がプロットされます．

ここでやっていることは初期角度0.3[rad]，初期角速度0.0[rad/s]の初期状態から制御トルクが常に0の時のシミュレーションをbody.fdyn(ほにゃらら)で実行しています．”.nofriction”はリンク間の衝突を無視するための設定を行っています．

fdynの引数はfdyn(シミュレーション時間,制御トルク,初期角度，初期加速度)となっています．

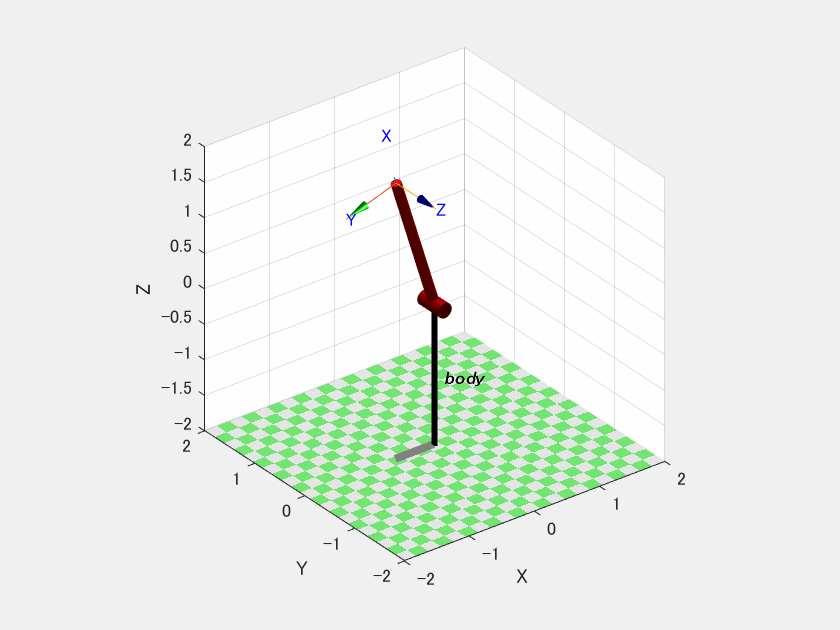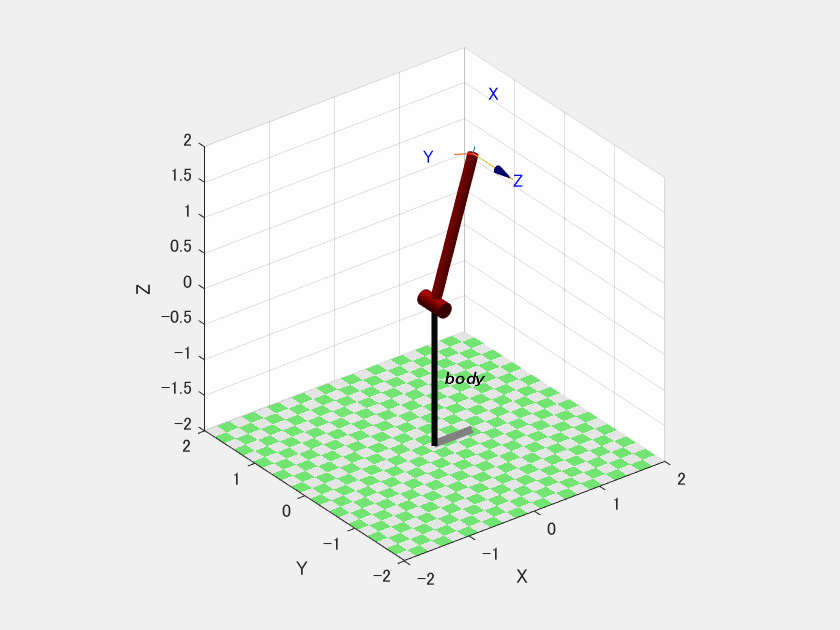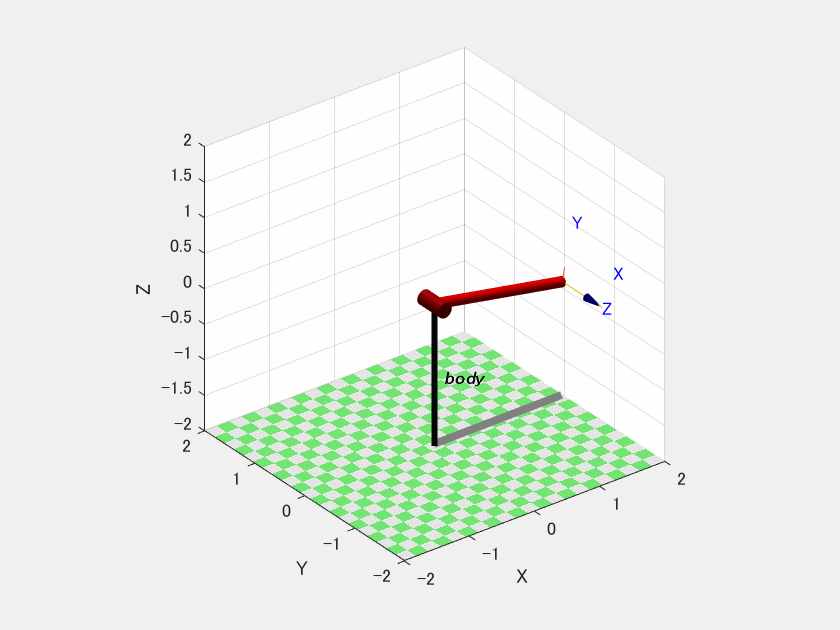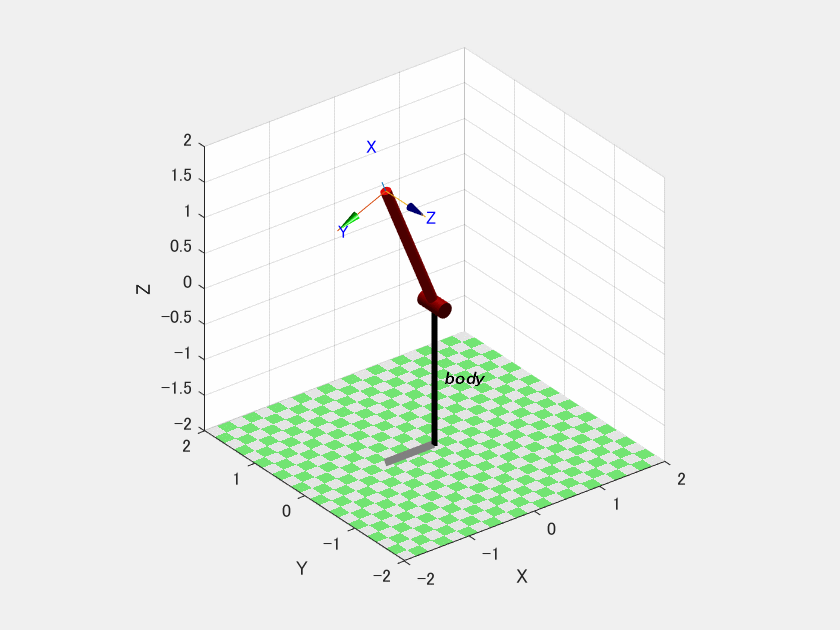
一見ちゃんと動いてます．これが本当に正しく動いているかを自分で勝手に作成したプログラムを使って検証していきます．

自作2次元シミュレーションとの比較検証

まず自分で2次元で一様な質量をもつ剛体の棒振り子のシミュレーションを作成しました．このとき振子のパラメータはRobotics toolboxで作成した3次元に対応するものを使用しました．

コード3: Robotics toolboxを使わずに2次元の振子シミュレーションを作成

% シミュレーション1(ode45を使ったシミュレーション)
Theta = [0.3 ;0]
tlim = [0 10]
[t2,y] = ode45(@SIP,tlim,Theta);

% シミュレーション2(オイラー前進差分でシミュレーション)
dt = 10e-5;
Theta_ts = Theta;
t3 = 0:dt:tlim(2)-dt;
for ind = 2:tlim(2)/dt
   dThetadt = SIP(t3,Theta_ts(:,ind-1));
   Theta_ts(:,ind) = Theta_ts(:,ind-1) + dThetadt*dt;
end

%ローカル関数　今の角度を入力すると角度の微分と角速度の微分が返ってくる
function dThetadt = SIP(t,Theta)
% SIP model for ODE45
%t: time
%Theta: [theta; omega]
m=60;%[kg]
g=9.81;
h=2.0;%[m]
I = (m*h^2)/3;%棒の端点からの慣性モーメント

dtheta = Theta(2);
domega = m*g*(h/2)*sin(Theta(1))/I;
dThetadt = [dtheta;domega];
end

Robotics toolboxの内部ではode45という常微分方程式を解く関数でシミュレーションを行っています．私はあまりode45に詳しくなかったのでode45を使ったシミュレーションとオイラー前進差分を使ったシミュレーションの2つで検証しました．

その結果，ほぼ一致することが確認できました（青〇と赤線が一致）．これで少なくともz軸回りに関わる設定について正しく設定できることがわかりました．

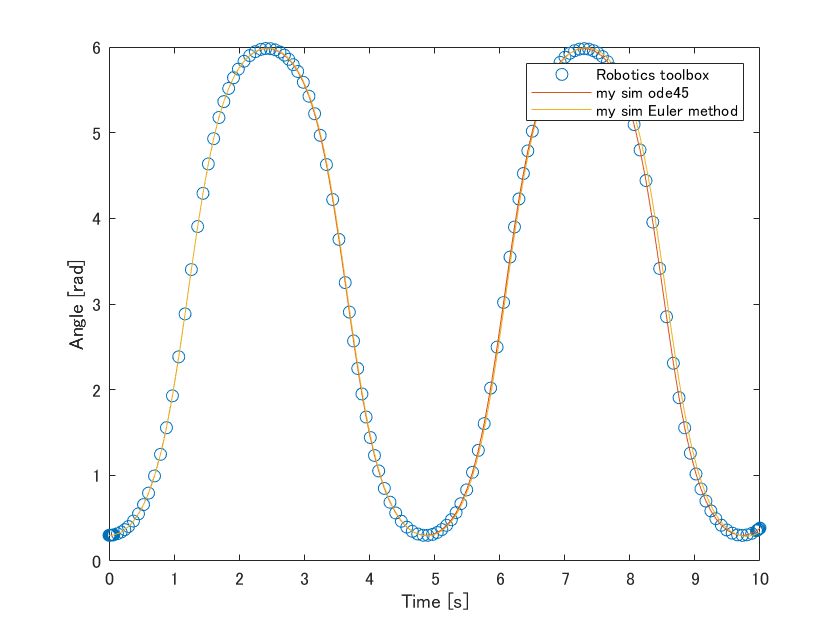
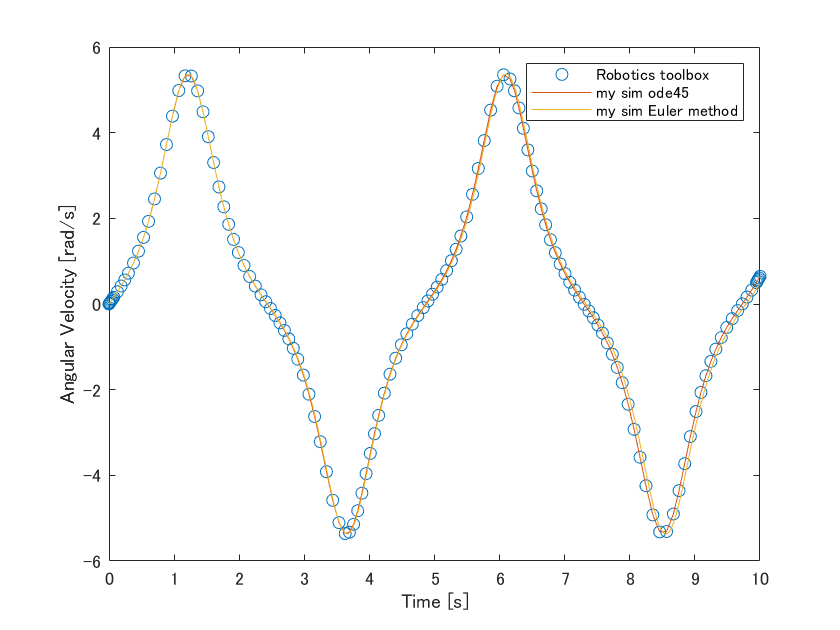
おまけ1: 常微分方程式を解いてくれるode45について

おまけでオイラー差分のdtを変えて試したところ，ode45は十分に精度がよく，オイラー法における時間ステップdtを小さくするほどode45に近づくこともわかりました．また，ode45は今回のシミュレーションでは0.01等の角度から開始すると少し結果が安定しないこともありました．

おまけ2: 自作SIP関数の説明

重さが\(m \mathrm{[kg]}\)，重力加速度が\(g \mathrm{[m/s^2]}\)，リンク長が\(h \mathrm{[m]}\)でリンクの中心\(h/2\)に重心がある一様な棒の倒立振子の運動方程式は

\[I\ddot{\theta} = mg(h/2)\sin \theta\]

ここで\(\theta\)は鉛直上方からの角度です．この時，この一様な棒の端点回りの慣性モーメント\(I\)は

\[I=\frac{1}{3}mh^2\]

です．

運動方程式は2階の微分方程式ですがそれを1階の連立微分方程式の形で表すと

\[\dot{\theta}=\omega\]

\[\dot{\omega}=\frac{mg(h/2)\sin \theta}{I}\]

となります．

この式がSIP関数に書いてある式です．