皆さんは離散フーリエ変換(Discrete Fourier Transform, DFT)結果の絶対値\(|c_k|\)とパワースペクトル(PS),パワースペクトル密度(PSD)の違いを知っていますか.この記事では以下の結論を理解して,これらの3つの使い分けができるようになることを目標に解説しています.
結論:定常信号について調べるときはDFTの結果やPS,確率過程について調べるときはPSDの図を作成する
まず,これらの違いを
\[x_1 = 2\sin(2\pi t)\]
\[x_2 = 2\sin(2\pi t) + \zeta, ただし\zeta は平均0分散1の正規分布に従う乱数です\]
の二つの時系列について異なる時間長\(T_1=10 s\)と\(T_2=100 s\)でフーリエ級数の絶対値,パワースペクトル,パワースペクトル密度を計算することで示したいと思います.この時系列は100 Hzのサンプリング周波数で作成しました.つまり\(T=10\)秒間で\(N=1000\)個の点からなっています.
最初に本記事で扱う離散フーリエ変換について定義します(離散フーリエ変換の定義はいくつかありますが今回はmatlabのfft関数の定義と同じものを採用しました).
\[X(k) = \sum_{n=1}^N x(n) \exp(-\frac{2\pi i}{N}(n-1)(k-1))\]
ここで\(n\)は離散化した時間,\(k\)は離散化した周波数で\(t=n\Delta t, f=k\Delta f\)という関係があります.
この定義を見てわかるように\(X(k)\)は離散フーリエ変換に使用した時系列の長さ\(N\)が長いほど値が大きくなることがわかります.そのため,時系列の長さ\(N\)の影響を消すために\(N\)で割った,複素フーリエ係数に対応する\[c_k =X(k)/N \]をプロットする際には使用するのがいいと思います.そのためこの記事では\(c_k\)を離散フーリエ変換の結果をプロットする際などに使用していきます.
複素フーリエ係数\(c_k\)の絶対値とPS,PSDの違い
それぞれの値(y軸)の意味
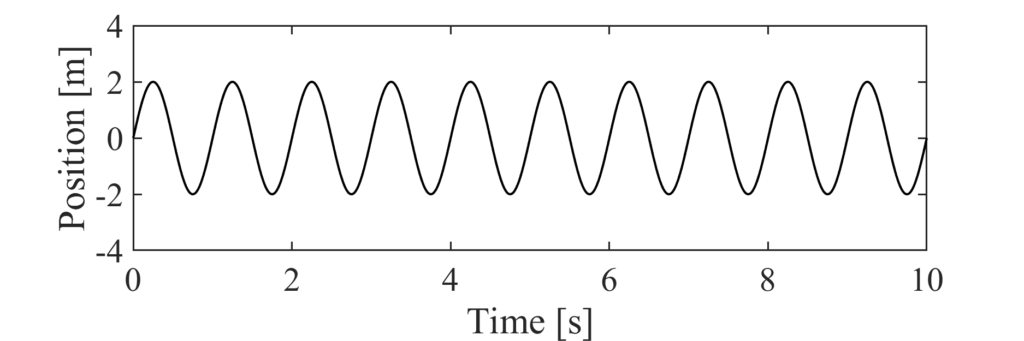
振幅2 m,周波数1 Hzのsin波\(x_1\)について,FFTをおこない\(|c_k|\)やPS,PSDの図をプロットしました.図をからわかるように \(|c_k|\) ,PS,PSDはどれも\(10^0 =1\) Hzにピークを持っていることがわかります.
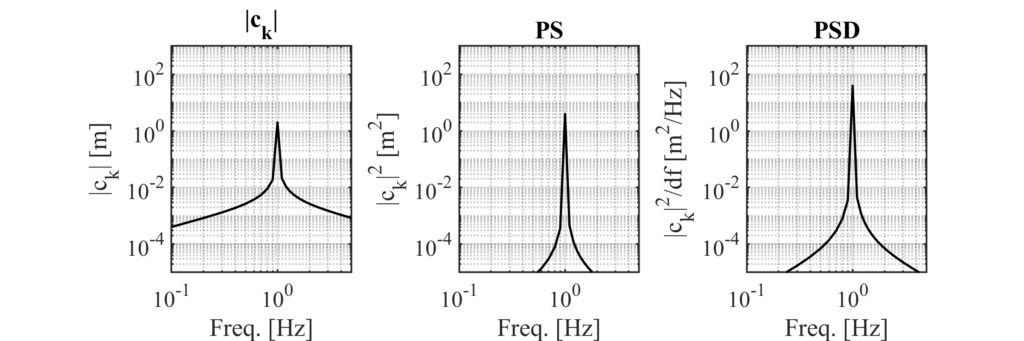
おもに異なる点はピークの高さです.
\(|c_k|\) はフーリエ級数展開した時の係数の絶対値なので信号の振幅に一致します.今回の場合は振幅2 [m]がピークの値になっています.
パワースペクトル(PS)は式で書くと\(|c_k|^2\)です.そのためピークの値は\(2^2 = 4 \mathrm{[m^2]}\) となっています.
パワースペクトル密度(PSD)は式で書くと\(|c_k|^2/\Delta f\)です.ここで\(\Delta f = 1/T\)で使用した時系列の長さ\(T\)によって決まる周波数分解能です.
補足(読み飛ばし可)——————————————————
\(X(k)\)を使ってPSDを書くと
\[|c_k|^2/\Delta f = |X(k)/N|^2/\Delta f \\
= |X(k)|^2/N^2\Delta f \\
=\Delta t^2 |X(k)|^2/T\]
ここで\(\Delta t=T/N, \Delta f = 1/T\)です.
するとコメントで指摘いただいた数式が出てきます.
\(\Delta t^2\)がかかっている部分が異なりますが\(X(k)\)の定義に\(\Delta t\)を含めるか含めないかの違いが出ているだけだと思われます.
実際にスペクトル解析ハンドブック(P28, ペリオドグラムの章,リンクはAmazon)では\(X(k)\)の定義に\(\Delta t\)を含めたもので定義されていてそれを\(X'(k)=\Delta t X(k)\)とするとPSDは\(|X'(k)|^2/T\)になります.
補足終了——————————————————————
つまり,今回は\(T = 10\)を使用したのでピークの高さは\(2^2/(1/10) = 4 \times 10 =40 \mathrm{[m^2/Hz]}\) となります.また,数式からTが変化するとピークの高さも変わってしまいそうだと予想できます.
なんだかPSDよりもPSや\(|c_k|\)のほうがわかりやすくていいように感じます.
どうしてパワースペクトル密度なんてものを計算するのでしょうか.
実はPSDは特定の周波数のピークの高さ(点)ではなく,複数の周波数にわたる値(線)として意味を持つような信号に注目して解析するために計算するものなのです.例えばホワイトノイズなどがそれにあたります.ホワイトノイズをフーリエ変換するとすべての周波数領域で一定の値を持ち,ピークの値ではなく周波数領域全体でどのような値をとるのかがホワイトノイズの性質を知るうえで重要になります.
そのため,例として先ほどのsin波にホワイトガウシアンノイズを加えた信号において|c_k|やPS,PSDがどのような値になるのか見ていきます.
ノイズの有無による影響
以下の2つの信号について考えます.

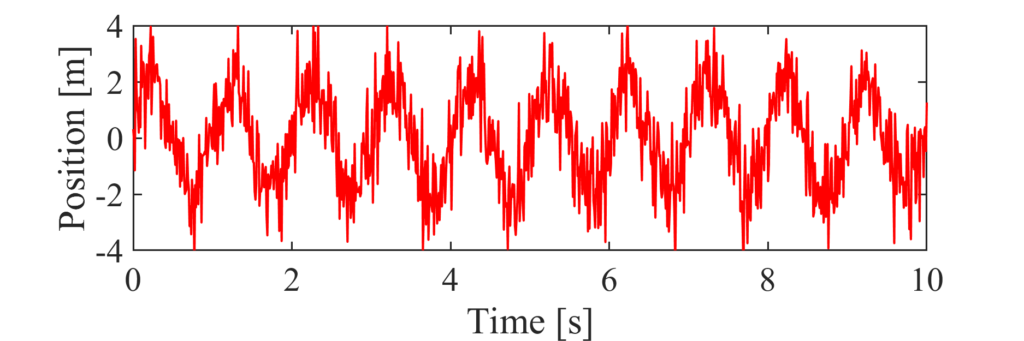
ノイズなしに加えて,ノイズありはsin波の周波数である1 Hz以外の点でもパワーを持つようになっています.これはホワイトノイズをフーリエ変換するとすべての周波数でパワーを持つことに対応します.
でもよく見ると\(|c_k|\)やPS,PSDはベースラインの高さがそれぞれ違いますね.特にPSは小さいように思います.実はPSD以外はデータ長Tを変化させるとベースラインの高さも変化してしまいます.以下でそれを示します.
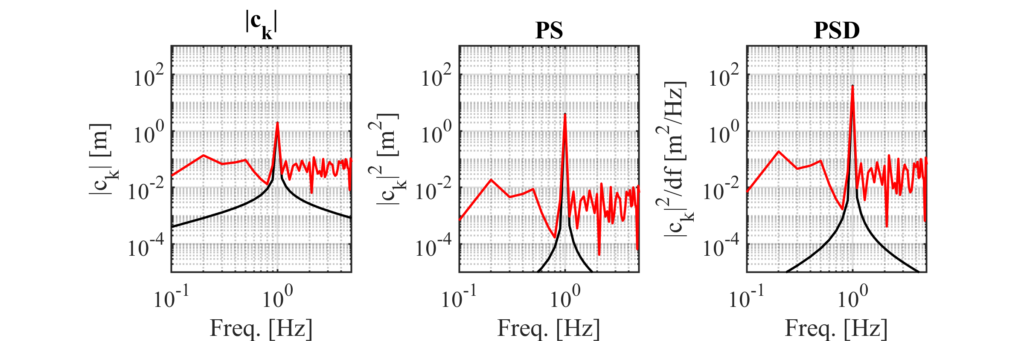
時間長の変化による影響
ノイズありの場合にT=10 s (黒線), T=100 s (赤線)で\(|c_k|\)やPS,PSDを計算した結果を以下に示しています.
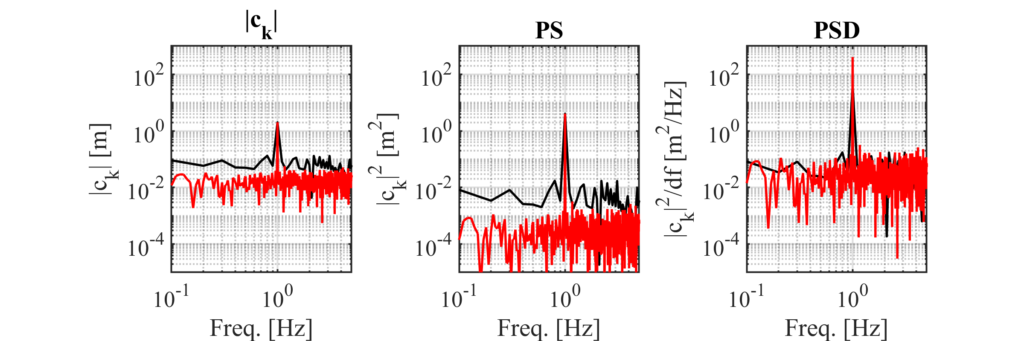
図を見るとわかりますが\(|c_k|\)とPSはベースラインの高さが変化しているのに対してPSDは使用した時系列の長さが10 sから100 sに変化しても一定の値になっていることがわかります.
使用した時系列の長さによって高さが変化してしまうということは,図を見たときにPSの場合は計算に使用した時系列の長さを知らなければどのような分散のガウシアンホワイトノイズが加えられているかわからないことを意味します.
逆に1 Hzにおけるピークの高さは|c_k|とPSでは時系列の長さが変わっても同じですが,PSDでは100 sの時系列のほうが高くなってしまっています.つまり,PSDを見ただけでは正しいsin波の振幅を求めることができないことを意味します.
よって以下のようにまとめられます.
まとめ:定常信号を調べるときはPS,確率過程を調べるときにはPSD
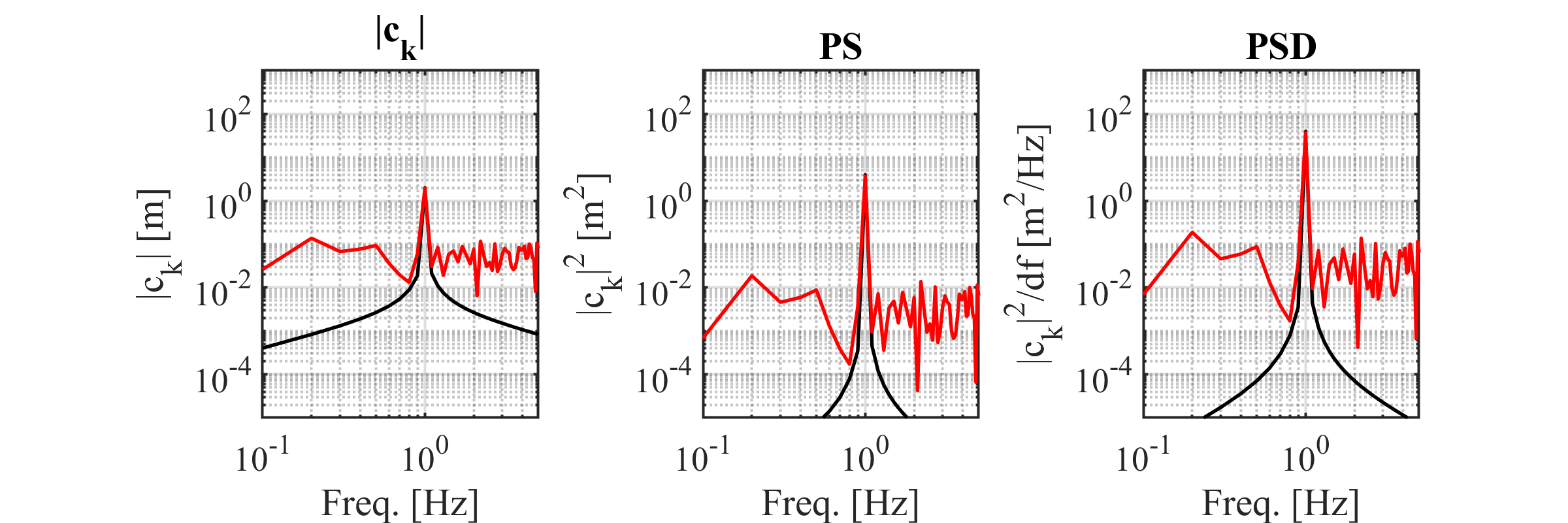
例えばですが,下図のような信号があった時に,どんなsin波(定常信号)であるのかに注目して話す時はPSを図示し,どんなノイズが乗っているのか(確率過程の性質)に注目するときにはPSDを図示するのがよいということがわかりました.

更新履歴
2021/03/08 Pさんのご指摘に基づき記事の内容をより正確な内容に更新しました.
2022/09/06 PSDの数式について補足を追加しました

コメント
地震学の実習で、疑問に思っていたことがあったのですが、理解できました。
分かりやすいですね。
sさん,コメントいただきありがとうございます.理解の助けになれたのでしたら幸いです.
パワースペクトル密度(PSD)は式で書くと|X(f)|^2/Δf と書かれていますが,これは誤りで,|X(f)|^2/Tのはずです.PSDはパワースペクトルを周波数Δfで割った密度ではなく,”単位周波数あたりのパワー”を周波数Δf で割ったものになります.
Pさん,ご指摘いただきありがとうございます.
確認して修正いたします.反映まで少しお時間ください.