ラプラス変換の気持ち
なぜラプラス変換を学ぶのか?
端的に言うとラプラス変換は微分方程式を誰でも解けるようにするツールである[1].
微分方程式は物体の運動,電気回路,化学反応など自然界の現象を記述する際に必要不可欠で多くの場合その解を知ることが重要となる.
微分方程式をそのまま解く場合,解の一般形を代入したりする必要があり,その形が思いつかない人には解くことができない.
ラプラス変換を使用すれば特定の手順で手を動かしさえすれば誰でも解けるのである.
つまり微分方程式の民主化である(東北大学の大関先生の表現[1].私も好きな表現).
今回の目標
・ラプラス変換ができるようになる.
・ラプラス変換表の形に数式を変形できるようになる.
ラプラス変換の定義と理由
\(f(t)\)を\(t\geq0\)に対して定義された\(t\)の関数とする.
このとき\(f(t)\)のラプラス変換を\(\mathcal{L}[f(t)](s)\)で表し以下のように書ける.
\begin{align}
\mathcal{L}[f(t)] = F(s) = \int_0^\infty f(t) \exp(-st) dt
\end{align}
\(s\)は一般に複素数だがその実部は正.
▼小ネタ微分方程式を解くときの流れ
以下のようなばね定数\(k\)のばねの先についた質量\(m\)の質点の運動方程式を例題として考える.
2行目の式は初期条件である.
\begin{align}
m\frac{d^2}{dt^2} x &= -kx, \\
x(0) = 1, &\frac{d}{dt} x(t)|_{t=0}=-2
\end{align}
両辺をラプラス変換する
ラプラス変換対応表を参考にすると
\begin{align}
\mathcal{L}\left[m\frac{d^2}{dt^2} x\right] &= \mathcal{L}\left[-kx\right], \\
m\left(s^2X(s)-sx(0)-\frac{d}{dt}x(t)|_{t=0}\right) &= -kX(s), \\
m\left(s^2X(s)-s \times 1-(-2)\right) &= -kX(s), \\
\end{align}
次に\(X(s)\)についてまとめる.
\begin{align}
ms^2X(s) – ms +2m &= -kX(s), \\
(ms^2+k)X(s) &= ms – 2m, \\
X(s) &= \frac{ms – 2m}{(ms^2+k)}, \\
X(s) &= \frac{s – 2}{(s^2+k/m)}
\end{align}
この式の両辺を逆ラプラス変換すると左辺は\(x(t)\)となり,右辺が微分方程式の解となる.
ラプラス変換対応表にある形になるように変形(部分分数分解など)する
今回の数式は別に分母を分解しなくても以下のようにラプラス変換対応表にある形にすることができる.
\begin{align}
X(s) &= \frac{s – 2}{(s^2+k/m)} \\
&= \frac{s}{(s^2+k/m)} – \frac{2}{(s^2+k/m)}\\
&= \frac{s}{(s^2+k/m)} – (2\sqrt{m/k})\frac{\sqrt{k/m}}{(s^2+k/m)}
\end{align}
ラプラス変換対応表をみてX(s)->x(t)へ
ラプラス変換対応表から
\begin{align}
x(t) &= \cos \sqrt{k/m}t – 2\sqrt{m/k}(\sin \sqrt{k/m}t)
\end{align}
| \(f(t)\) | \(F(s)\) |
| \(1\) | \(\frac{1}{s}\) |
| \(t\) | \(\frac{1}{s^2}\) |
| \(t^n\) | \(\frac{n!}{s^{n+1}}\) |
| \(e^{at}\) | \(\frac{1}{s-a}\) |
| \(\delta(t)\) | \(1\) |
| \(\sin(\omega t)\) | \(\frac{\omega}{s^2+\omega^2}\) |
| \(\cos(\omega t)\) | \(\frac{s}{s^2+\omega^2}\) |
| \(f(t)\) | \(F(s)\) |
| \(\frac{d}{dt}f(t)\) | \(sF(s)-f(0)\) |
| \(\frac{d^2}{dt^2}f(t)\) | \(s^2F(s)-sf(0)-\frac{d}{dt}f(t)|_{t=0}\) |
| \(\int_0^t f(t) dt\) | \(\frac{1}{s} F(s)\) |
| \(e^{at}f(t)\) | \(F(s-a)\) |
逆ラプラス変換の定義を使った計算はしない?
逆ラプラス変換は複素積分として以下のように定義される.
\begin{align}
\mathcal{L}^{-1}[F(s)] = f(t) = \frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty} F(s) \exp(st) ds
\end{align}
この複素積分は留数定理によって計算することができる.が実際に逆ラプラス変換する際にはラプラス変換対応表を使用することが多い.
ラプラス変換の練習
練習1:
\begin{align}
f(t) = \left\{
\begin{array}{ll}
0 & \mathrm{for}\ t < 0 \\
t & \mathrm{otherwise}
\end{array}
\right.
\end{align}
練習2:
\begin{align}
f(t) = \left\{
\begin{array}{ll}
0 & \mathrm{for}\ t < 0 \\
e^{-at} & \mathrm{otherwise}
\end{array}
\right.
\end{align}
逆ラプラス変換の練習
練習1:
\begin{align}
X(s) = \frac{s-2+1/s^2}{s^2+1}
\end{align}
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p862-
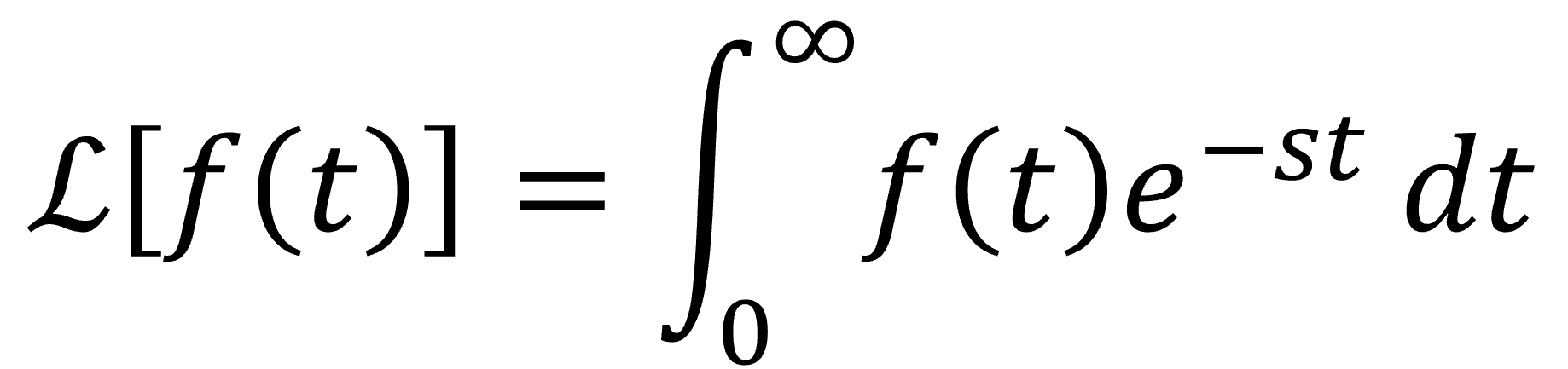


コメント